Building a benchrest rifle

[Lee Martin]

Feb 8, 2016 20:00:21 GMT -5 squawberryman said:

Lee has it always been a given that barrel harmonics were so closely monitored? If not, what year is it agreed they came into play and what did the group sizes go from-to? A different way to look at this question is like the guy that invented the rubber worm for bass fishing, did someone just take the BR world by storm one dat after "getting it"?

Deflection properties have been understood for decades. Even as far back as Harry Pope, or the late 19th century. Now triangulating harmonics, loads, and velocity is a different story. It really wasn’t until the early BR set published articles in the 1950’s that load tuning took root.

Let me also be clear about the process. Barrel harmonics can’t be measured without sophisticated, and very expensive equipment. The best we can do at the range is alter loads and study the targets. Big vertical suggests sine wave transition. Tight, consistent groups with little vertical suggests we’re on a node. ‘Suggests’ being the pivotal word. We have no way of proving exit is at deflection tips.

Refining these principles has definitely helped shrink aggregates. Then again so has better barrels, bullets, optics, powders, stocks, bedding techniques, and wind flags. The game constantly evolves and as Mike Ratigan so eloquently put it, "benchrest is all about balancing razor blades".

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Bullet Making – Part II
_____________________________

It’ll be a month and a half until my dies are ready. In the interim I'm submerged in the study of crafting precision bullets. Whether that’s literature, benchrest forums, or phone conversations I’m all ears. The wait has also afforded me the chance to collect supplies. Two must haves were purchased this week. The first is a rock tumbler which will clean & lube the components; namely the cut cores and jackets. These aren’t directly placed in the rubber drum. Instead they’re poured into mason jars along with the lube or solvent. The sealed glass is then rotated in the tumbler.



Mason jars – these are mainstays in my house (and many other homes throughout the southeast)



I’ll need to firmly hold the jackets for core placement and beyond. A lot of guys drill delrin sheets with 0.250” holes. Sizes range from 100 to 500 and some feature sliding tops. This allows the cores to be gently agitated into the cups. Efficient but the thought of standing in front of my Bridgeport for hours boring plastic is, well boring. I can’t say I’m the first to stumble upon these but Smartreloader’s 22 LR / 25 ACP boxes are perfect for 6mm. They hold 100 shells and are priced under $4.00. I purchased ten.

0.820” 6mm jackets:







-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Calculating Ogive
_______________________________

The 68 gr Ultras I’m shooting are flat base, dual radius bullets. They start 9 ogive in the rear and blend to 6.5 up front. Eventually I’ll discuss this design and others used in short-range BR. Until then I thought it would be interesting to show how ogives are derived.

Commercial bullet manufacturers publish ballistic coefficients and sectional densities (SD). Many benchrest brands are hand formed and vary in weight, curvature, and the tip diameter. We rarely cite BCs or SDs, instead focusing on jacket length, weight, base type, and ogive. The first three are readily apparent whereas the ogive isn’t.

Computing a bullet’s fundamental geometry:

1) Calculate the sectional density SD

SD = (Weight in grains) / (7000) * (diameter)^2
My Bart’s Ultras mic 0.2435” at the pressure ring
SD = (68) / (7000) * (0.2435)^2 = 0.1638

2) Calculating the ogive

L = length of the ogive nose from base to tip
D = diameter of the base of the ogive
T = diameter of the ogive tip
R = radius of the curve of the ogive in inches

To find the radius of the ogive:
R = Sqr(L) / (D – T) + (D – T) / 4
R1 = Sqr(L)
R2 = R1 / (D – T)
R = R2 + (D – T) / 4

To find the length of the ogive:
L = SqRt(R * (D - T) - Sqr(D - T) / 4)
L1 = Sqr(D - T)
L2 = L1 / 4
L3 = R * (D - T) - L2
L = SqRt(L3)

To find the diameter of the ogive tip:
T = D - 2 * R + SqRt(4 * (Sqr(R) - Sqr(L))
T1 = Sqr(R) - Sqr(L)
T2 = SqrRt(T1 * 4)
T = D - 2 * R + T2

To find the diameter of the ogive base
D = T + 2 * R - SqRt(4 * (Sqr(R) - Sqr(L))
D1 = Sqr(R) - Sqr(L)
D2 = SqrRt(D1 * 4)
D = T + 2 * R - D2

Ogive is the forward curved area between the bullet tip and base. That curve is the segment of a circle with radius “r”. Ogive simply denotes the number of calibers required to equal that “r” value. So a 7 ogive 6mm has a circular arc segment with r = 1.701” (7x 0.243”).



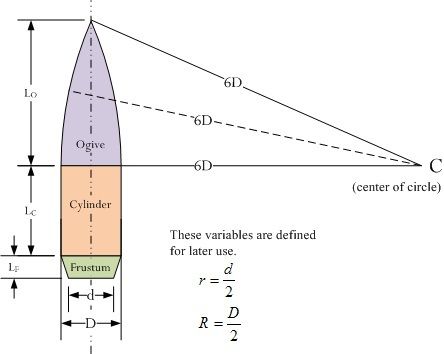
Ogive profiles are either tangent or secant.



* Tangent ogives – body of the bullet and ogive radius intersect at a single, tangent point

* Secant ogives – body of the bullet and ogive radius intersect at two points, neither of which are tangent to the base

Secant ogives impart less drag and offer higher BC’s. The trade-off is they’re more sensitive to seating depth. Many dual radius bullets, known as hybrids, use both tangent and secant curvatures. The tip which engages the rifling is tangent, the section between the shank and tip is secant.

If it weren’t for its double radius I’d show the calculation using a 68 gr Ultra. It gets messy though because even with an optical comparator it’s tough pinpointing the 9 to 6.5 transition. Instead I’ll share a chart guys used back in the single-ogive days:



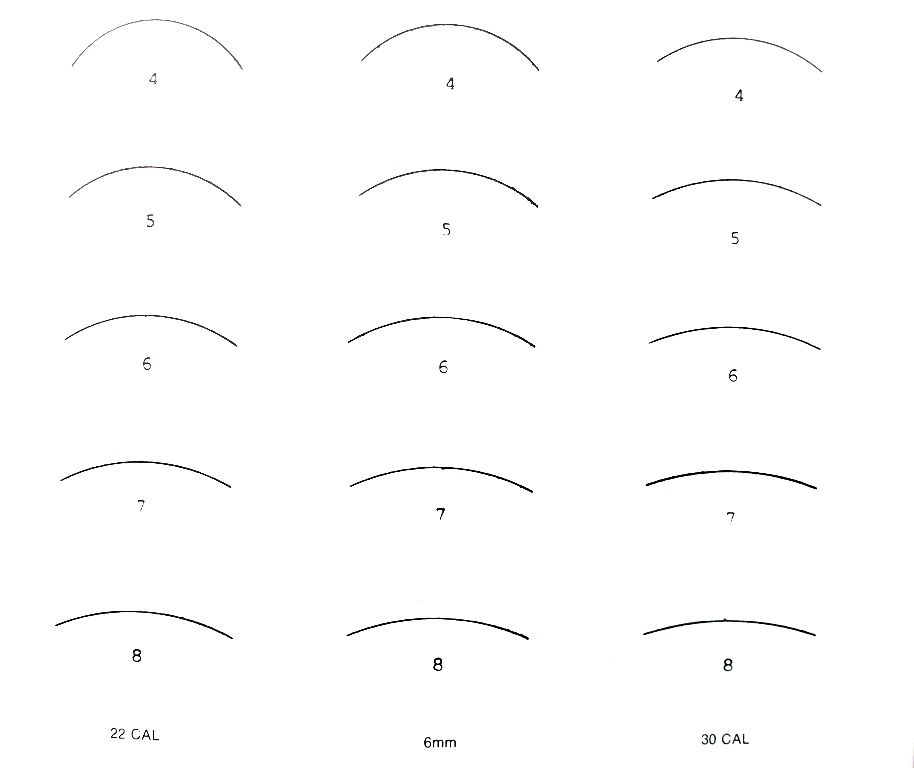
You’ll see these are caliber specific and mimic the curvatures. By overlaying the bullet under magnification shooters found which ogive it best fit. This isn’t too scientific but does eliminate the need for involved math. Let’s test the chart with a single-radius design.

Berger, 52 gr Match Grade .22-caliber:



Using the above equations:

L = length of the ogive nose from base to tip = 0.476”
D = diameter of ogive base = 0.224”
T = diameter of the ogive tip = 0.057”
R = radius of the curve of the ogive in inches = ?

R = Sqr(L) / (D - T) + (D - T) / 4
R1 = Sqr(L) = 0.689
R2 = R1 / (D - T) = 1.319
R = R2 + (D - T) / 4 = 1.361
Ogive = R/D = 6.076

According to our calculations the Berger is a 6 ogive 22-cal. Overlaying it on the chart confirms this. Even if we didn’t have the chart we could make one. Merely take a compass, like the ones we had in elementary school, and set the radius to 1.361”. Then draw the arc. It’ll give you a twenty-two 6-ogive profile. Reversing these equations lets us create different ogives by caliber. Meaning we'd start with the known values of R, D, and the desired tip diameter. With 3 of the 4 inputs in hand we'd figure the length of the nose.

I realize this forum caters to the revolver crowd. But these principles absolutely apply to handgun bullets:



I’ve spent a lot of time studying these shapes, particularly the LBT series. Using rudimentary math, our optical comparator, and a micrometer, we can document (and duplicate) the precise geometry. When time permits I’ll do the analysis on bullets dropped from LBT molds (teaser – there’s nothing magical about their noses. They’re wonderful slugs but contain basic ogives, whether they be single or dual radius). More to come.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Reloading 6 PPC – Part I
________________________________

The way we reload 6 PPC is not unlike other rifle cartridges. But subtle differences do exist, mostly around tolerances and cleanliness. I’ll detail those differences and the process end-to-end. What follows will enhance any form of precision reloading; this isn’t limited to short-range BR.

Spent primers are first knocked out with a Wilson kit. Put a shell on the base, slide the punch through the flash hole, and gently tap the rod. Many do this outside the FL sizer so carbon and anvil fragments don’t foul the press.





Powder residue is removed using 0000 steel wool lightly rotated around the neck:







Inside neck carbon is thinned with one pass from a nylon brush. We don’t want to clean down to bare brass, a little carbon is good. Instead we’re eliminating loose particles stuck to the wall.





A primer pocket brush cuts carbon around the flash hole.

Before cleaning:





Just insert and rotate:



After cleaning. These tools are rather effective. The pocket you see here is on its 19th reload.



Case length is closely monitored. Long necks apply more bullet pull, short necks apply less. We want tension identical shot-to-shot. I trim mine 1.490” on the nose.



Brass seldom grows in a tight chamber PPC. Every five to six firings I may true the necks 0.0005 – 0.001” but that’s it. This is done with a Wilson micro-adjust trimmer and Sinclair base.



I’ll post part 2 in a day or so.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Reloading 6 PPC – Part II
_______________________________

Fifty de-primed and cleaned cases:



Before sizing I randomly mic neck thickness. If you recall they were initially turned 0.0095”. Tight chambers, proper headspace, and sound bolt lug bearing reduces brass movement. These still run 0.0093 – 0.0095” after 18 firings, only shedding a tenth or two. But a word of caution – always measure the neck with a seated bullet. Wall thickness times two plus the bullet diameter isn’t fool proof.



Full length sizing is one of the most challenging and misunderstood aspects of the PPC. By design benchrest chambers are cut extremely tight. This promotes better bore alignment, extraction, and case life. But that’s all for naught if the brass isn’t sized properly. Sizing techniques and theories have evolved since the 1950’s. Decades ago competitors neck sized and shoulder bumped leaving the body as is. Only when extraction got sticky or the bolt clicked did they squeeze the base. Another trend was the fitted neck. In that scenario neck clearance was so small you didn’t even resize it. Pop the primer out, add a new one, pour powder, and seat a bullet. The amount of brass rebound created enough tension for the next load. Fitted necks required total clearance well under 0.001”. These tricks worked OK for milder rounds like the .222 and 6x47 but are ill-advised with the 6 PPC. Its operating pressure is just too high. Nowadays most full-length size between firings.

I use a dedicated press for this rifle. Mine is a Harrell’s and it’ll clamp about anywhere.

In my gun room:



At the range:



I prefer sizing and priming at home. It saves time and is one less piece of equipment to drag along.

FL dies - the sizing die must match your chamber!!! In short-range BR we don’t order sizers from catalogs. Off the shelf dies may work enough to cycle but they aren’t ideal...far from it in fact. Best practice is to fire-form your brass 2 – 3 times and send samples to a die maker. Linwood Harrell out of Salem, VA and Jim Cartensen in Bellevue, IA are two I recommend. They’ll take your cases and create the proper die. That die should do the following:

• Size the body-to-shoulder junction no more than 0.001”
• Size the base at the 0.200” mark < 0.001”
• Bump the shoulder 0.001”

Jim Cartensen (JLC Precision) made mine, matching it to the 1046 reamer. The decapping pin/expander ball assembly have been removed. I de-prime separately and shun expanders. All they do is kill neck concentricity. Tension is completely controlled by the bushings shown below:



Cutaway of Redding S die w/bushing. Here the decapper and expander are installed:



We begin by selecting the right bushing. Your decision is largely tied to the powder you shoot. LT-32, which is what I use, wants low pull. Other propellants such as Vihtavuori 133 need more, sometimes as high as 0.004”. My buttons range from 0.258” – 0.262”. I chose 0.261” for 0.0015” neck tension, calculated as:

[(wall thickness) x 2] + (bullet diameter) – (bushing size) =
[(0.0095”) x 2] + 0.2435” – 0.261” = 0.0015”

Seating a bullet confirmed the neck o.d. as 0.2625”. Coupled with my 0.264” chamber puts clearance at 0.0015”. The bushing is then inserted into the die. Next we have to fix the die in the press. And no matter what you were taught, screwing it down until it touches the ram and camming over 1/8 isn’t accurate. Nor is judging shoulder bump by closing the bolt on a dummy round. To precisely position the shoulder you need a bump gauge. A bump gauge is just barrel stub reamed for the shoulder and neck. A fired case is inserted and measured with a caliper. Always test more than one to be certain of the figure. My fired PPCs are 1.904”. So to bump the shoulder one-thou we tweak the die until the gauge reads 1.903”.



My sizer is fit with a PMA micro die adjuster. Each tick represents 0.001” and by splitting the marks you can fine tune to 0.0005”.



A test case is sized and checked in the bump gauge. I also mic the base at 0.200” before and after sizing. The JLC die reduced it 0.0006” which is perfect. Our body-shoulder junction is also assessed. Again, we want to decrease the diameter no more than 0.001”. Here’s a quick and dirty way to test this. Take your caliper and measure that line on a fired case. Be sure to wiggle it until it grabs evenly. Lock the caliper by turning the set screw. Size the brass and then slide the caliper over the body. It should stop about 1/8 of the way down. Illustrated:

Fired / unsized:



Sized



If the caliper hardly slips down the body you’re not sizing enough. If it goes well past 1/8 you’re sizing too much. If your die can’t meet these requisites get another die. Once the specs are in order the die is locked. The remaining shells are lubed with Imperial Die wax and sized.



I use an old K&M hand primer to seat the CCI BR-4’s. Fancier tools exist but I’m not convinced they net you much. I go by feel and set the primer a few thousands below the edge of the pocket.



Part 3 will cover powder throwing and bullet seating. Both of which are done at the range.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Reloading 6 PPC – Part III
_________________________

Seating depth – when I began with this PPC my baseline was touch. Touch is the loaded length at which the ogive kisses the rifling. It can be tedious to find. Here’s my process:

• Use a dummy cartridge. If you have to test with the real thing ABSOLUTELY REMOVE the firing pin assembly
• Seat a bullet way long under the neck tension you intend to shoot
• Take a match or lighter and smoke the bullet. This coats it with carbon. The matte black creates good contrast for the rifling marks
• Lube the locking lugs with bolt grease
• Measure the length in an ogive gauge. Jot down the number.
• Chamber the round. The bullet is pushed back into the neck as it meets the rifling.
• Remove the cartridge and re-measure with the ogive gauge. Label this “jam length”. Also observe the engraved marks. They’ll be distinct and long
• Clean the bullet with 0000 steel wool, screw your seating stem down 0.003”, and again smoke the nose.
• Chamber it and check the newly formed marks under a 6x loop. Continue these steps until the marks become really faint. At that point go down in 0.001” increments until they’re barely visible (but noticeable under magnification). This is what I call touch. Write down the ogive gauge length and seating stem number.



Base-to-ogive measurement:



Rifling marks after being jammed



Example – when my barrel was fresh, touch equaled 2.357” on the ogive gauge. This translated to #35 on the seater. To jump the bullet 0.005” I’d dial #30, or 2.352”. To load 0.005” into the lands I’d move to #40 or 2.362”. You get the idea. Over time throats erode and touch has to be re-evaluated. 950 firings caused this point to grown a few thousandths in my rifle. Because finding touch is slow going I recently switched to a jam reference. Meaning I baseline the jammed measurement, not touch. Current jam length is 2.368” after closing on a 2.375” dummy. The bullet is being pushed 0.007”. I’ll test at jam and then move the bullet back in three-thousandth steps for a given charge. I’m still collecting data but the gun performs well 0.003” & 0.006” off. Groups at minus 0.009” and 0.012”, while decent, aren’t as tight as jam -3 and jam -6. Eventually I’ll seat to -0.050” and see if a pattern emerges.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Reloading 6 PPC – Part IV
______________________________________

I pour powder and seat bullets at the range. This allows me to adjust loads as the atmosphere changes. Tied to this is data I’ve collected over the past six months. Cross-referencing it tells me what charge and seating depth the gun liked for a condition. But you must be flexible when tuning. Because a load once did dots in 50 degrees and 40% humidity doesn’t mean it always will. Your records are only a starting point for the surroundings.

My Culver measure clamped to the bench.



H.L. Culver invented the metering insert in the 1950’s. Up until 1994 he produced around 1,000 for the Lyman 55 unit. My dad helped him machine and assemble the last 240. #31 shown here pre-dates our involvement; hell it even pre-dates me. In the 1970’s he stopped numbering them for reasons I can’t recall.



The powder is poured into the case. I’ll leave detailed discussions of the measure, other models, throwing techniques, and volume versus weight for later.

Components are arranged on the bench for ease of loading:



Primed and charged brass is placed on the seater base:



The body is slid over the shell and a bullet is dropped in the top:



The adjustable stem is added and seating is done in an arbor press. The handle’s feel tells you a lot about neck tension. After doing hundreds of these you’ll know when tension is off. More resistance means more grab, less resistance signifies lower bullet pull. Those become foulers and I inspect the brass when I get home.





I randomly check the loaded neck diameter. My chamber is 0.264” and I aim for 0.2625” on the cartridge. This nets 0.0015” total clearance.



A better view of the arbor press and LT-32 powder jug



950 down this tube and it still shoots. These targets are from last Saturday – 27.7 grs LT-32, jam minus 0.003”.

0.386” – 0.243” = 0.143”





0.421” – 0.243” = 0.178”





Saturday’s eight group agg equaled 0.218”.



-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[cmillard]

nice shooting.

[Lee Martin]

Cutting Groups – Part X
________________________________

I’ve posted a lot of good targets in the “Cutting Groups” segment. It’s about time I share one that isn’t much to look at. And this glob is all on me.

When shooting free recoil you must be still. Whether hunched over the stock or upright watching the flags, don’t move until the butt hits your shoulder. It’s just too easy to bump the gun, the rear bag, or both. This PPC tracks beautifully, largely due to the McMillan Edge. Touch the 1.5 oz trigger and the scope tells me if I did my part. Illustrated:

I hold 6 o’clock on the mothball:



At firing the stock slides ~1/2” and stops on my shoulder. Proper tracking is confirmed by seeing this through the reticle.



The cross-hairs go up a tad and there’s no horizontal. Push the rifle against the fore-end peg and we’re back to 6 o’clock. Minor dial adjustments may be required but they’re small.

Saturday I had four shots in the right portion of the group shown below. Center-to-center it was in the 1’s. Then on the fifth I didn’t keep my head down, coming up as my finger met the trigger. It was just enough to nudge the rear bag and the scope proved it.



Here’s the group. The hole on the left was pulled due to gun handling, not the wind. It scored 0.356”.





What may have been had I stayed still



-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Cutting Groups – Part XI
_____________________________

“The only sure way to avoid making mistakes is to have no new ideas” – Albert Einstein

Unlike the firing pin fiasco I had a positive glitch last Saturday. It began with my micro seater dialed to jam minus 0.003”. When loading the first bullet I immediately knew something was wrong. The arbor press’s travel was short and there was no resistance. Sure enough only 0.020” of the base protruded into the mouth. I checked the Sinclair top, the die body, and even measured the bullet’s ogive. On those fronts everything was fine. Then I noticed the seating stem was wobbly. The retainer had loosened causing the shaft to float:



Relative to the neck, this approximates the seating depth:



My friend Boyd Allen is always telling me “don’t be afraid of the extremes, just as long as they’re safe”. I loaded a few more and shot a group. With such mild neck tension the rifling had no trouble seating the bullet. This was confirmed when closing the bolt. It cammed into battery with little effort. The first group, laid down in switchy conditions, was tight:



I loaded more shells and set a new target. Same long seating depth, same switchy wind. Group #2 was another nice mid-1’s cluster. The rifle just drilled shot after shot. Maybe the stars had aligned and it wasn’t the hard jam? I answered that by tightening the stem returning to previous lengths (jam-0, jam-3, jam-6). High 1’s and low 2’s followed. Nothing to sneeze at but they couldn’t match the first two. I went full circle and again loosened the stem for minimal seating. That group recorded 0.146”.



Now this loading practice is not uncommon to benchrest. Using the lands to seat bullets goes back decades. All that's required is very light tension and an OAL way ahead of jam. But I may never have tried it if not for the stem snafu. So from one loose screw I gain another tuning path.

Note - I recommend putting more than 0.020" in the neck. Unloading one of these during a match cease-fire could stick it in the rifling. Meaning you’d pull primed brass and have a chamber full of powder. Jam plus 0.020” to 0.030” may be a good starting point. Or if jam is halfway down the neck, load a quarter in and have the lands push the bullet back to 1/2.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[Lee Martin]

Bullet Making – Part III
_____________________________

The bullet dies and presses arrived today. Once they’re set-up I’ll post pictures. I also decided to build a dedicated swaging bench. Material cost ran $40 and it is fairly stout:



You’ll see the core cutter mounted to the right edge. This one is homebuilt and I’ll cover how it works later on.



Minus the presses and dies, here are the components needed to craft benchrest bullets.



I should be up and running within a week. A step-by-step guide will soon follow.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[newrugersafan]

Can't wait to see what all is involved in the process. Looks like you need good ventilation.

Thanks Lee

Mike

[Lee Martin]

Bullet Making – Part IV
_________________________________

Here are the George Ulrich dies. The first is the core swager (aka, “squirt die”) and it’s made from steel. The second is the core seater, the third is the point-up die. Those are carbide:



The punches. Top to bottom:

• Core swaging punch
• Core seating punches – 0.2110”, 0.2115”. 0.2120”, 0.2125”, and 0.2130”. These must be matched to the jacket. The appropriate size is 0.0005” under the jacket’s inner diameter.
• Point-up punches



At first I asked for two presses. I planned on using one for core swaging and core seating. The second would be dedicated to point forming. But I changed my mind and just ordered a third. That way I can set the dies and never worry about losing adjustment when swapped. It should arrive in the next two weeks.

Core squirting press mounted:



Auto-ejection top:



A view of the punch and converted ram:





-Lee
www.singleactions.com
"Chasing perfection five shots at a time"

[cherokeetracker]

Good looking press. The modifications look solid, and well made. I like the way you think. I agree with ordering a third press. I hope you can get started with some of the process, and begin, getting that learning curve behind you. I am looking forward to your success with this endeavor.

Charles

[Lee Martin]

Apr 6, 2016 19:57:18 GMT -5 cherokeetracker said:

I am looking forward to your success with this endeavor.

You and me both Charles. And I'll start documenting the process real soon.

One other thing to mention here. Anyone interested in making competitive bullets should find a mentor. There's a lot to learn and with the dies alone costing in upwards of $3,000, it's an investment (time and money). George Ulrich is 1 of 3 guys producing carbide dies capable of winning in BR. If you go lower cost and choose steel, throw Larry Blackmon's name into the mix. But this is a very small circle. I've never dealt with the others but George Ulrich is first-rate. By phone he's shared a lot of tips, techniques, and bullet philosophy. In his words - "call me anytime with questions. I want you to succeed with these bullets". I hope to pass some of that knowledge along in this thread.

Mentor #2 is my dad. He used to make benchrest bullets in the 80's and 90's.

-Lee
www.singleactions.com
"Chasing perfection five shots at a time"